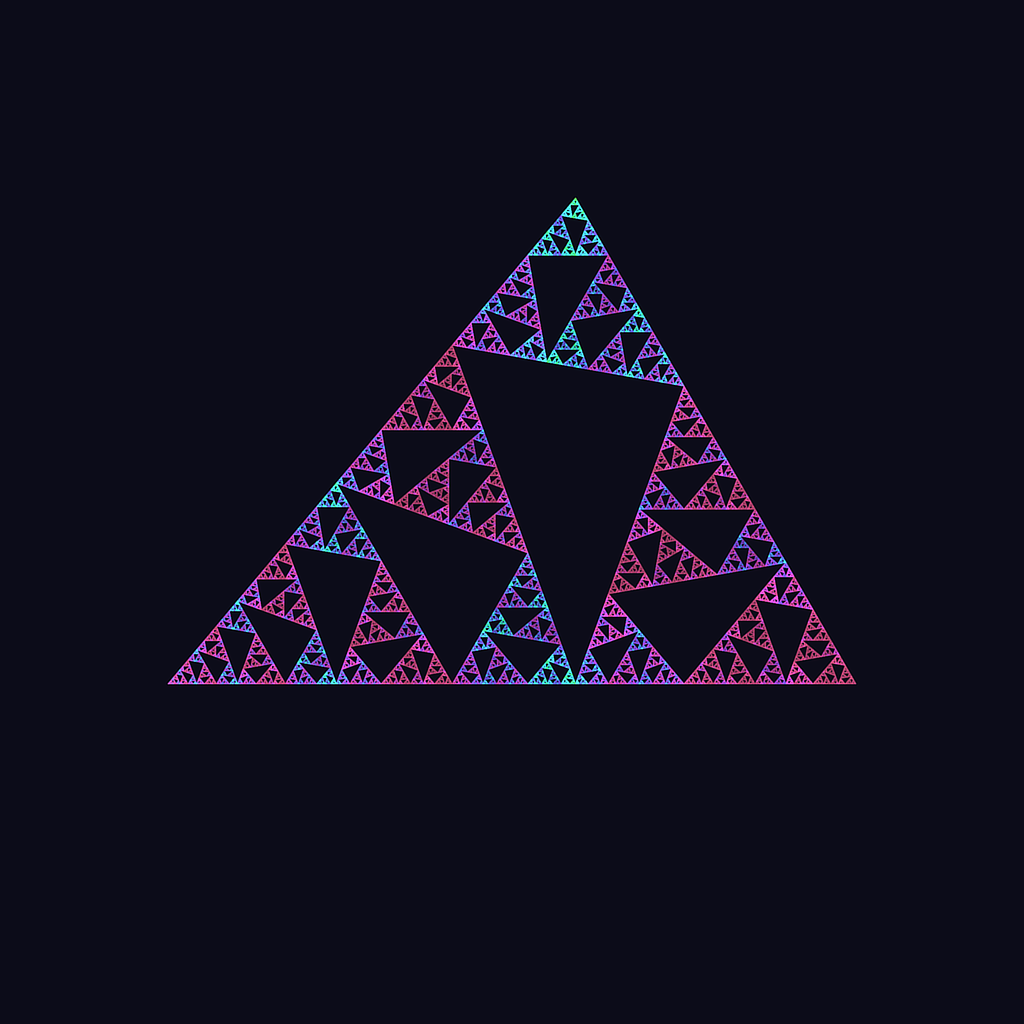In the previous post about making text in Chaotica, I introduced the Sierpiński Gasket. I got a complaint about it not being centrally symmetrical. So I decided to make a version of the Gasket that will annoy those preoccupied with symmetry. As always here’s the code. Try and see what it does and how it works if you feel like it.
| A | B | C | |||
|---|---|---|---|---|---|
| Post affine | |||||
| A | B | C | D | E | F |
First off, let's answer the more important question: what is a gasket? My dictionary tells me it's supposed to be 'a flat piece of soft material or rubber that is put between two joined metal surfaces to prevent gas, oil or steam from escaping: The gasket has blown'. This seems to be a bit of a misnomer for an immaterial object that certainly isn't put in between something and with its infinite holes would surprise me if it could prevent anything liquid from ever escaping. Despite the misnomer, I do think fractal gaskets are beautiful and do not blow. Googling gasket leads to images that faintly resemble fractal gaskets. Another term often used is the Sierpiński sieve. The fractal could actually be a nice sieve that sorts grains of sand and has infinitely many hole sizes. On top of that, it also has a classy ring to it and from here on out, I will refer to gaskets as sieves.
Now we got that out of the way we can start answering the question on how to construct the fractal. Intuitively the sieve can be constructed using scissors by removing the same structure as the structure we had at the start, but flipped, rotated and scaled (note that these operations are exactly what affine transformations can do). What's left is three scaled-down versions of the original triangle. Now repeat this ad infinitum.
IFS operate on a pixel level. For IFS it is not a matter of cutting entire pieces out, but a matter of never reaching certain areas, a.k.a the void. With the exception of the first few iterations (due to the possibility of choosing a starting point that does not lie within the set), you will never reach some parts of the triangle. These parts do not belong to the set. Convince yourself by trying. For illuminating reasons, I give in and post the equilateral Sierpinski sieve. But only because this version makes it easy to spot the congruent little triangles it is made up out of. Each angle is 60 degrees. Each void is the same shape as the whole triangle, but scaled down twice and rotated. Because each angle is the same we don't have to worry about flipping operations.
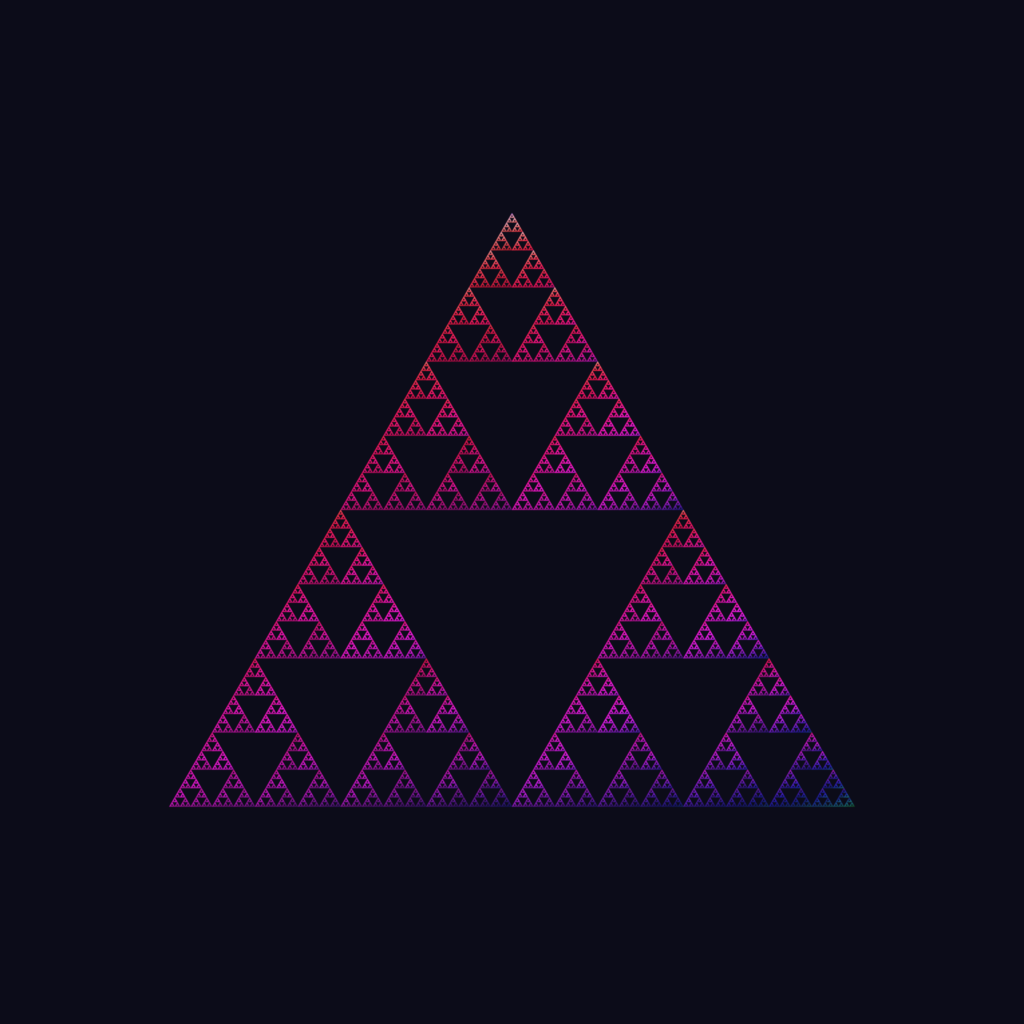
Can this function set be generalised? According to the paper Sierpiński pedal triangles by Ding et al. it can. The general form is (don't forget to set your calculator to degrees):
![\[F_0(x,y)=\begin{bmatrix}cos^2(B) & cos(B)sin(B)\\cos(B)sin(B)& -cos^2(B)\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}\]](https://matigekunstintelligentie.com/wp-content/ql-cache/quicklatex.com-6e401bd9d4acc7e165d07f7661d88729_l3.png "Rendered by QuickLaTeX.com")
![\[F_1(x,y)=\begin{bmatrix}cos^2(C) & -cos(C)sin(C)\\-cos(C)sin(C) & -cos^2(C)\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+\begin{bmatrix}sin^2(C)\\cos(C)sin(C)\end{bmatrix}\]](https://matigekunstintelligentie.com/wp-content/ql-cache/quicklatex.com-d5233d3b3f17bb54512ff90d4debfd98_l3.png "Rendered by QuickLaTeX.com")
![\[F_2(x,y)=\begin{bmatrix}-cos(A)cos(C-B) & cos(A)sin(C-B)\\cos(A)sin(C-B) & cos(A)cos(C-B)\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+\begin{bmatrix}sin^2(C)\\cos(C)sin(C)\end{bmatrix}\]](https://matigekunstintelligentie.com/wp-content/ql-cache/quicklatex.com-6bb094ed94fd27d994a30eb67e2a38d9_l3.png "Rendered by QuickLaTeX.com")
This is where things start to get wonky. What if you use other values than three 60 degree angles? Below I used 50, 60 and 70 respectively. It's less obvious, but the void leaves three congruent triangles yet again. There's mathematical proof though it's easier to just take out your geo triangle to convince yourself once more. Can we recreate the sieve from the previous post? Unfortunately, we can't with this formula, it collapses to an ordinary filled triangle. It's not wonky enough. I encourage you to try other wonky values. Like what evens happens when the angles don't add up to 180? That would be crazy and should never be attempted.
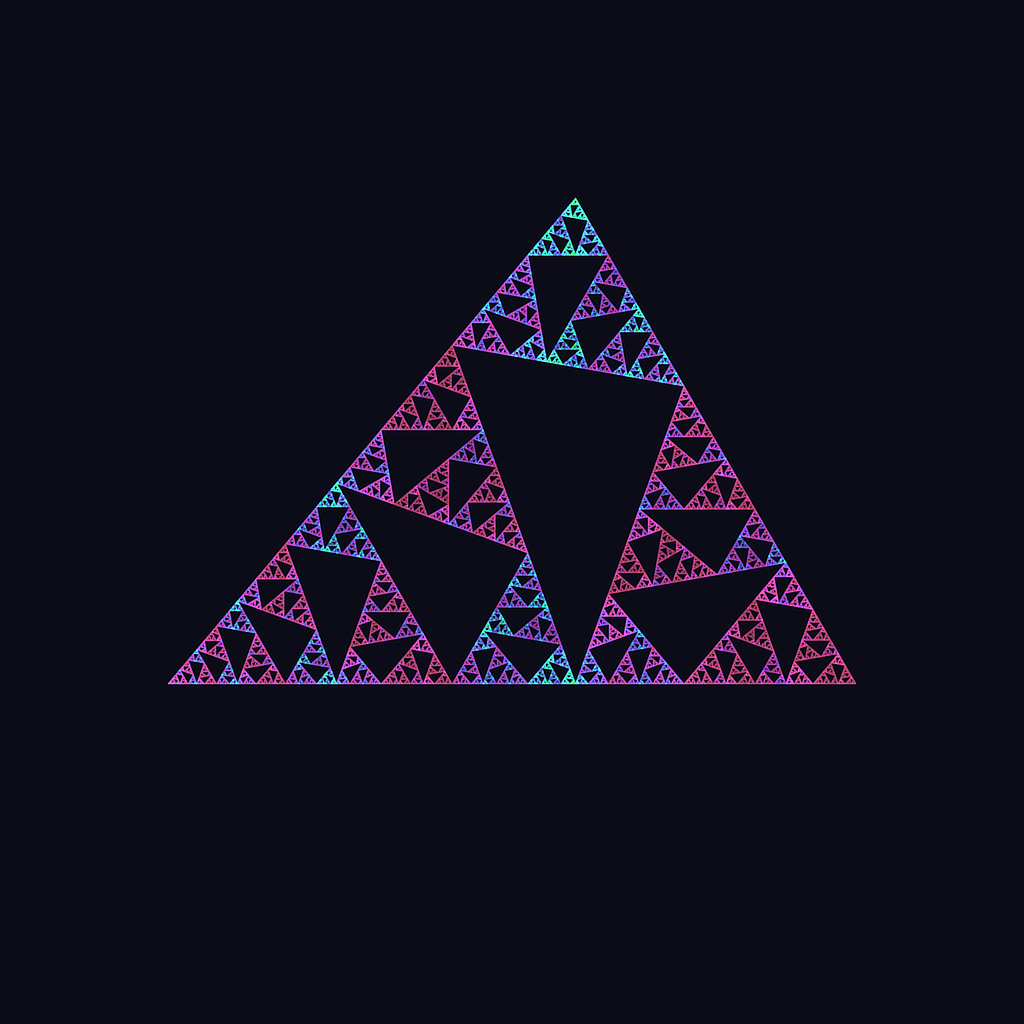
Hope you enjoyed it! Spotted a mistake, please let me know at matigekunstintelligentie@gmail.com