Category: Articles

Enter fullscreen mode for the full fullscreen experience

The past few months I’ve been experimenting with printing my work. On canvasses, posters and even masks. Figuring out how many dots per image are needed, which colours work, which parts are cut or folded. Here are some gifts I gave to people that doubled as little experiments.

• 

• 

• 

• 

• 

• 

For those interested, here’s a list of works that are currently available. Some featured in my blogs and some from a blog post in the making. More works can be found on my Instagram @matigekunstintelligentie. Expect more algorithms in my blogs that allow you to make your own art pieces! Have any questions or want to commission me? Email me at matigekunstintelligentie@gmail.com!

In a previous blog, I asked the question of whether names are somehow connected with certain faces. CLIP projects text and images to the same latent space. I decided to see what happens if the names Karen and Kevin are projected into the StyleGAN2 latent space and then visualised by the generator. I must admit that the samples are slightly cherry-picked. Entering a single name is a slight abuse of the method which normally expects a little more elaborate description. Nevertheless, enjoy!

• 

• 

Kevin has experienced some shit. Probably due to the self-fulfilling prophecy of Kevinism. In the previous blog on ideophones, the figure on the right was also named Kevin only second to Damien. Neither of these Kevin’s look like the Kevin that I have in mind.

I pity the manager this Karen is talking to. I also wondered what Matige Kunstintelligentie personified would look like. Note that CLIP is trained in English and that these Dutch words will unlikely be part of the vocabulary. English is very easily tokeniseable whereas Dutch has compound words like Kunstintelligentie. I wonder whether that has a significant impact on Dutch NLP.

This technique of generating faces with CLIP and StyleGAN2 from names definitely needs some polishing work. As stated before this is not the intended use of CLIP. However, with a labeled dataset it could be done. If someone is willing to (legally) scrape some database with names I will happily train the model that does this. Then we might truly find out who is most Karen or Kevin.

How did I make the interpolation at the end? A magician never reveals his secrets. Luckily I’m no magician. The answer is quite simple: I trained a StyleGAN2 model. When I trained the model I had, and as of writing still have, a single 1080 GTX. The 8GB memory on this machine has caused me quite some trouble with training. The stats on Nvidia’s original GitHub page also aren’t very encouraging. They estimate that it would cost 69 days and 23 hours of training on the FFHQ dataset in configuration-f with a single Tesla V100 GPU. The 1080 GTX has less memory and 69 days is a bit much. What to do? How about transfer learning?

The concept of transfer learning is simple. A network spends most of its time learning about low-level features. These low-level features are similar across many imaging tasks. So instead of training a network from scratch, we leverage the effort that has already been put in training the low-level features on another dataset, in this case, FFHQ, and train on another dataset. This dataset can anything you like, but keep in mind that you’ll need quite a bit of data. FFHQ has 70k images! Recently a new paper call ‘Training Generative Adversarial Networks with Limited Data‘ came out, which might help if you don’t have a lot of data. This will likely be the topic of a future blog.

In my case, the dataset came from a paper called ‘A shell dataset, for shell features extraction and recognition‘ by Zhang et al. Hats of to Springer Nature for making science publicly accessible for a change. The data can be downloaded here. The dataset needs some cleaning. Using some simple thresholding I centered each image and removed the background. There’s another problem: FFHQ images have a resolution of 1024×1024, but these images are way smaller. Even in this day and age, people are taking low-resolution photos, unfortunately, presumably to save disk space or to annoy data scientists. I ended up upscaling the images with an AI technique, I don’t remember which one but any will do. Now that we have the data I’ll introduce the code.

Nvidia’s ProGAN/StyleGAN papers are brilliantly executed but an eye-sore to look at code-wise (to me at least). The codebase is fairly involved compared to other ML projects. It’s long, has some custom CUDA functions, and is written in TensorFlow. I tried TensorFlow in 2016, had a terrible time, switched to Pytorch, and never looked back. If TensorFlow is your thing then go to Nvidia’s official repository (you will need to clone this repository anyway so you might as well check it out) and follow the instructions there. I will be using Rosalinity’s implementation. You can read through Rosalinity’s instructions instead if you want, besides some minor tweaks it says the exact same.

First, you need to create a Lightning Memory-Mapped Database (LMDB) file from your data. As described in the repository you can generate multiple image sizes. I only need 1024×1024 images. The dataset path is the path to your dataset (who would have thought) and the LMDB path is where the resulting file will be stored. All this information is also available on Rosalinity’s repository. One thing it doesn’t say though is that your dataset folder must contain subfolders with data. If you pass a folder without another folder inside it, it will think the folder has no images.

python prepare_data.py --out LMDB_PATH size 1024 DATASET_PATH

Download the FFHQ f configuration .pkl file from the Nvidia repository and also clone the repository. Use the following command to convert the weight from pickle to Pytorch format. ~/stylegan2 refers to the Nvidia repository.

python convert_weight.py --repo ~/stylegan2 stylegan2-ffhq-config-f.pkl

Normally you’d now start generating faces and nothing is holding you back from doing so, but I want shells not faces. To get shells we train on the shell LMDB file. Compared to the training command from Rosalinity you’ll only need to change three things: the checkpoint, model size, and batch size. You can also choose to augment your dataset by mirroring the image over the y-axis. Shells are mostly dextral or right-handed, so mirroring the images may bias the data a little, but not many people will notice hopefully.

 python train.py --batch 2 --size 1024 --checkpoint stylegan2-ffhq-config-f.pt LMDB_PATH

I set the batch size to 2 because that is all my poor 1080 GTX can handle before it runs out of memory. From here on out it’s a waiting game. The longer you train the better the model becomes up to a certain point. After training, you can generate samples with the following command. Note that the checkpoint is not stylegan2-ffhq-config-f.pt but your own checkpoint!

python generate.py --sample N_FACES --pics N_PICS --ckpt PATH_CHECKPOINT

This video shows what happens during training. It was trained on a dataset of shell illustrations. Some of you might have noticed Richard Dawkins pop up at the start. This wasn’t a coincidence. Take a lot at projection.py to project your own images into the latent space.

“The word ‘onomatopoeia’ is also an onomatopoeia because it’s derived from the sound produced when the word is spoken aloud.” – Ken M

Imagine ringing up a caveman. Utter astonishment on both ends of the line aside, what would you talk about? What could you even talk about? Without the accompanied pantomime it may even be impossible to convey a message, made up out of regular words, that is received in full fidelity in this situation. It’s hard holding a conversation that transcends time and space solely through the medium of sound. Certain sounds, however, are and will consist of similar sound waves regardless of whether they are perceived here and now or during the construction of the pyramids of Giza. Likely you would use sounds mimicking sounds from nature like thunder or bird calls. Some onomatopoeia might be understood as they resemble a sound but not quite.

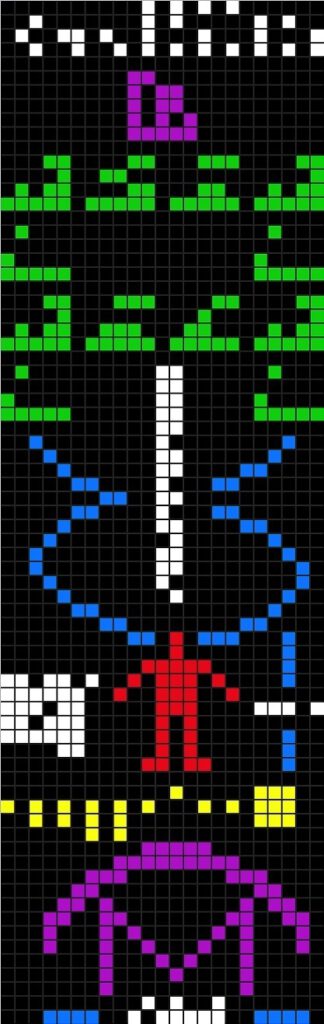
Fart jokes are considered low hanging fruit to some. But in my opinion, their universality and timelessness are unmatched. From the Japanese in the Edo period to Mozart and Aristophanes, fart jokes are understood by everyone (at least humans) throughout all ages. Reportedly Mozart was obsessed with farts and even wrote songs about them. Using sound to convey a sound is what makes a fart joke so easy to understand. If you wrote down a joke it wouldn’t make people laugh that can’t read the joke. Sound is powerful in that regard. Although maybe not as powerful as the visual medium. The Arecibo message is a message meant to be received by other intelligent life forms. It was transmitted through radio waves but carries a visual message. Can we use sound to convey a visual message in other ways?

Wolfgang Kohler observed exactly this when he performed an experiment where he presented people with two figures, one jagged, one rounded, and two names: Takete and Baluba. He then asked which name belonged to which figure. A strong preference for calling the rounded shape Baluba and the jagged shape Takete was found. This seems to indicate that humans have to ability to convert a sound into a visual idea.

In 2001 a similar experiment was repeated under Tamil speakers in India. The Tamil language uses many ideophones, words that elicit an idea in sound, on a daily basis. In the case of onomatopoeia, a sound evokes the idea of another sound. In Tamil, these ideas can also be different perceptions like visual ideas. Ideophones are uncommon in western languages, but we do have a few such as zigzag or blob. The shape of the letters may have something to do with this, but I ain’t no linguist.

Another ideophone is the conceptualisation of a whole personality when hearing a name. ‘Recently’ this has become a meme in the form of Karen. Karen is someone that ate a whole burger and decided not to like it and now wants to speak to the manager for a refund. Everyone knows a person like this and many people think that the name Karen fits the bill. This concept isn’t completely new. The name Kevin in Germany is associated with a low-achieving person, usually from a lower-class background. It’s a vicious cycle where Kevins, for whom this is not true, are discriminated against and are met with low expectations. It is possible for a Kevin to not be a ‘Kevin’ but the prophecy tends to fulfill itself for these reasons. This is called Kevinismus.

Do some names better suit particular faces than others? Do people have a preference? In order to test this, I propose the following two surveys. In the first survey, people are shown 10 faces, 5 male and 5 female, of non-existent people and are asked to come up with a name for each face. These names are then compiled into a list per face and a list of all male and all female names to sample from later. In the second survey, people are shown the same 10 faces with underneath each a list of 5 names of which 4 are randomly sampled from the list of all names and one is the most frequent name from the first survey. If some names really belong to certain faces we should see that participants choose the most frequent name more often than random chance.

This is exactly what I did. Posted my survey on r/samplesize and r/namenerds and celebrated a premature Burns night. A few hours later I checked in on the form and it had more than 200 respondents! Eventually, the survey would have an astonishing 1108 responses before I stopped taking entries to make survey number 2 (probably should not have done that during Burns night). After cleaning the data I quickly realised that I had a problem: Michael and Mark. Two faces had those names as their most frequent names. I might just mess this up later, I decided that each face would get the most frequent unique name instead. Let me introduce you to the names of the faces and the results!

Honourable mention: Lily Guardian of the Forest. In this case the data seems to confirm the hypothesis!

Honourable mentions: Dan glancer of surreal gallery, Skebep Bernardo. Here the top choice came second.

Honourable mention: Baby Karen. Here the fifth place was randomly sampled and overtook the top choice. This face has some elements commonly associated with ‘Karen’ mainly the hair-do, but not quite everything. Nevertheless Karen was the third most frequent entry.

Honourable mention: Garret imposer of dreams. I messed up. I should’ve included the top mention in the second survey here, instead I accidentally entered Michael instead… Nevertheless ‘Michael’ does very well in the second survey. One explanation as to why ‘Mark’ was chosen so many is times is that this face may resemble Mark Cuban a little (maybe/probably I’m very wrong).

Honourable mentions: Jean Pierre commiter of war crimes, goodwill Jared Kushner. Here I went with John as the name among random samples. ‘John’ was outranked by ‘Robert’ and ‘Patrick’.

Honourable mentions: Supreme leader Annette of the Czech Republic, Mandy Microkrediet. ‘Michelle’ hit it out of the park.

Honourable mentions: Bob teller of dad jokes, generic chef #5. ‘Gordon’ was a big succes. As the last honourable mention alludes to, this face may resemble chef Gordon Ramsey.

Honourable mention: Guptar possesor of worldly riches. Here I went with ‘James’, which didn’t do so well. ‘Marcus’, the 4th name in the first survey seems to be more fitting.

Honourable mention: grandma Deborah conveyer of bed time tales. ‘Susan’ is an enormous succes!

Honourable mention: grandma Daisy baker of cookies. Margaret matched up very well. Susan was a good second and Karen made another appearance.

Bonus rounds

A whopping 89.1% ascribed the name Takete to the jagged shape, reaffirming the original hypothesis. 6.2% found that both names were equally fitting and 4.7% found Maluma a better fit.

This is the image that all started it off for me. The fisherman hat, the weird glasses, long sunkissed hair, and inebriated gaze. He strikes me as a ‘the Dude’ type of personality, but I didn’t have a name. From some comments on Reddit, I gathered that he bears a resemblance to the professional boxers Jake and Logan Paul. Personally, I’ve settled on Steve.

1. Jake 39
2. Logan 35
3. Chris 23
4. Kyle 23
5. Steve 19

Honourable mentions: Geoff but insists it’s pronounced phonetically, Master Leaf, Floombeard, Broderick, Slappy Whiskers, he calls himself Jagster, Shaggy from Scooby Doo, Broccolingus, Dude McBro the Alpha Surfer of Florida, Skane Skurr, Kyle’s midlife crisis, Lil Soggy, Jimbob, Child Boulder,

1. Damien 52
2. Kevin 29
3. Sid 17
4. Kyle 13
5. Damian 11

Honourable mentions: Shadowfax, Malachi Badson, Tony Pajamas, xX_69gamerjuice69_Xx, Helvetica, Smob, Discount Pennywise

Apparently Damian is a kid and son of the devil in movie Omen. Sid is also famously an evil kid in Toy Story.

1. Jason 24
2. Seth 23
3. James 20
4. Chris 16
5. Jack 16

6 people correctly found my real name: Rumpelstiltskin. Honourable mentions: Llanfairpwllgwyngyllgogerychwyrndrobwllllantysiliogogogoch, “I’m not mad, I’m just disappointed”, 5/10, “…you […] actually look less real than the other people…”, X Æ 12 ẞ, Facey McFaceFace, Cletus

Thanks, everyone for participating everyone! The blog is still a work in progress, the story is a bit all over the place and I probably abused a lot of jargon. The study could have been conducted better as some pointed out. I agree. I didn’t expect to get enough responses for even one name to be repeated twice. It can luckily easily be set up again. Many seemed to enjoy filling out the names nevertheless. If you have any suggestions either email me or shoot me a message on Reddit.

The images rendered in the browser from the previous posts don’t look anything like the images made in Chaotica. There are a few reasons for that:

• The number of iterations is comparatively low
• The colours are determined by fixed coordinates
• The previous colour of revisited pixels is not taken into account
• The image is not gamma corrected
• The image is not anti-aliased

• 

• 

The original flame fractal paper mentions that there is no correct number of iterations. Generally, the following maxim holds true: the more the merrier. For educational purposes, I slowed down the iteration speed and rendered each and every step individually. This way you can see how the Chaos game is played out. Once you understand the concept you of course want to speed things up. One of the biggest bottlenecks is rendering pixels at each step. The trade-off is between being able to precisely see what’s being rendered and speed. We generally don’t care about the former as much as by the maxim more iterations usually lead to better renders. But, we’d still like to see some progress. This allows users to cut the rendering process short if the intermediate render is not up to standard. For now, let’s update the image every 100.000 iterations. We can now massively increase the total number of iterations or even let the image render indefinitely shifting the problem to patience. You can experience the trade-off here (normally I’d have the implementation here in the article, but WordPress won’t let me for some reason).

• 

• 

• 

The colours in previous images were fixed per pixel coordinates. Whether a pixel is coloured after function x or y doesn’t affect its appearance. By introducing a colour for each function in the system and changing the pixel colour with a function that uses this colour we can change this. Whenever a function is chosen at random, its associated colour is also chosen. We want a pixel to reflect the path of colours it has traversed. One way of doing this is by taking the average between the current colour and the chosen colour. The current colour factor experiences logarithmic decay over time, until it is visited again.

   

Some areas of an IFS are visited more often than others. It would be nice if the frequency of visitation was reflected in the image. The first step is recording the frequency a pixel is reached in a buffer. You’ll also need to record the maximum frequency encountered over all pixels. You could then use the frequency divided by the maximum frequency to calculate the alpha channel of a pixel. More visited pixels then become more opaque. The issue with this technique is that certain areas are visited more than others. Looking back at the images from the first paragraph we see that the root of the tree is filled in nicely at a low number of iterations. The result of determining the alpha channel this way is that most parts of the tree would barely be visible. Applying a function that initially grows fast for low values and slow for large values would solve this problem. Taking the base 2 log of the value is a good choice.

After all these improvements the details may still be lost in darkness. To fix this a gamma correction should be applied to the alpha channel. A small gamma under 1.0 makes the image’s dark regions even darker. A gamma above 1.0 makes the image’s dark regions brighter. The gamma correction is done after rendering.

   

There’s one more point left. Anti-aliasing. If you zoom in on the image you’ll see these jagged lines that should be straight. This is called aliasing and it can be fixed. This topic, however, deserves an article on its own.

In high school, I thought that geometry was the most useless subject. It was mainly used to teach mathematical proofs that were supposed to be intuitive. They proved to be quite the opposite. If only my teachers would have shown that you need geometry to make fractals and games. I might have paid more attention. What follows is some simple high school level math which took me several hours to (re-)figure out. Of course, you can skip over the parts you already know.

First, we need Pythagoras' theorem: 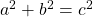. Which we can rewrite to find the length of the hypotenuse: 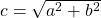. The visual interpretation theorem is nicely shown in the image below. The square at the root of the tree is attached to the hypotenuse of a triangle. Let's give the hypotenuse a length of . The area of the square then becomes 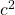. Similarly, the other squares of the triangle are given lengths of and 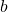. Pythagoras' theorem simply states that the area of the square attached to the hypotenuse is equal to the sum of the area of the squares attached to the rest of the right triangle.

The theorem is used to calculate the length of child squares. In this application, the lengths are calculated relative to a reference point 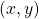. In the image above 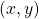is set a the point where the two smaller squares, which I'll call left and right, intersect. The length of the base square is set at 1. The lengths are thus given by:

   

   

To calculate the angle of these child squares in relation to the parent squares we need the SOH-CAH-TOA (SOS-CAS-TOA in Dutch) formulas. These formulas can be rewritten so that they solve for 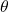. Which will be useful for the purpose of constructing a Pythagorean fractal tree. Here's a quick recap:

   

   

   

The angles are calculated as if the squares are turned counter-clockwise. To turn the right square we thus need to apply a negative angle. The angles then become:

   

   

Small digression into IFS formulas. In previous post I only used linear transformations. This means that the 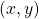coordinates remain unaltered after they undergo an affine transformation. The squares in the image are achieved by instead of returning the unaltered coordinates, returning coordinates that are uniformly sampled from a bi-unit square shifted 0.5 down and left.

   

   

Now because the first square is shifted 0.5 down and left we need some additional offsets.

   

   

   

   

Now all that is left is applying a scaling and rotation matrix. To chain operations simply matrix multiply the matrices.

   

   

Can something be deterministic, yet unpredictable? This is the question at the heart of chaos theory. Previously we’ve played the Chaos Game. If I were to give you a set of initial coordinates and a list of functions that are sequentially applied to these coordinates you would probably be able to eventually figure out the final coordinates. But if the functions were chosen at random you would not. Even though the random function is actually not random, but has an underlying deterministic function. In theory, you could, in practice you won’t.

Another thing that would make it impossible to figure out the final coordinates is when you start at an unknown coordinate. To illustrate this: imagine that someone is listing the digits of Pi. When this person starts out and you witness this start you, will be able to follow along and predict the next digit. You could use a deterministic spigot algorithm to do this. The only thing you need to keep track of is the number of digits the person has already listed. Alternatively, you could use a lookup table. If you were really fanatic, however, you would eventually run out of digits and you will have the use the spigot algorithm to get to more digits.

   

Pi is infinite and transcendental. Every subsequence can occur multiple times. If you were to tune in somewhere in the middle of the person listing its digits you would not be able to predict the next.

   

What is the next digit in this sequence? This subsequence of six nines occurs for the first time at the 762nd decimal point, also known as the Feynman point. But it also occurs at the 193034th decimal point. Without any context, there’s no way of knowing after which of the infinite subsequences you are supposed to continue.

Given that you’re far enough into the sequence, the digits of Pi can be seen as a pseudo-random number generator. Many things that appear random have underlying deterministic mechanisms. But due to tuning in at an unknown moment, you might not ever figure out what the underlying mechanism is.

The ancient Greeks also thought about this concept. Democritus illustrated the idea with a story of two servants that are sent to get water from a well at the exact same time. The servants would view their meeting as random. Unbeknownst to them, their masters concocted this evil plan. This story would have been a lot better if the masters had the servants walk out to the middle of nowhere from separate routes at the same time. This would have felt a lot more random to them. Of course, this example isn’t totally the same. The servants can easily deduce the underlying reason. The story would be more representative if the servants were mute and did not know sign language or how to write.

Loving Vincent is a movie very each frame was paintstakingly painted by hand. The film is from 2017, two years before the tool EbSynth entered the stage. Ebsynth lets you stylise keyframes and interpolates the rest of the frames for you. The film would’ve been finished much earlier if it were used, although it would be less impressive or even lazy.

How can we be even lazier? There is a technique called style transfer. The name is quite illuminating. It lets you transfer the style, let’s say that of Vincent van Gogh, to any picture you like. This means you wouldn’t even have to paint each keyframe by hand!

Loving Vincent is about the death of Vincent van Gogh. The last painting ever painted by van Gogh was the painting ‘Boomwortels’ or Tree Roots. Recently the location of the subject of this painting was rediscovered on a postcard. The photo of the tree roots on the postcard was taken from a different perspective. What would happen when we transfer the style of the painting to the postcard? Could this be a scene that Vincent could have painted if he were still alive?

• 

• 

Looks pretty good! Now note that style transfer does not take semantics into account. It does not know what a tree or a guy with a bike is. Guys with bikes should be the same colour as bushes in neural network world. What about something more relevant? Masks are everywhere these days. Naturally, Vincent would also have worn one in our time. I’m not a Photoshop buff, and as stated before, I’m definitely not a painter. So how about style transfer once more?

• 

• 

Not bad. Here I applied style transfer to the Photoshopped image using the style of the original. You can unfortunately still see my bad Photoshopping, especially on the upper right part of the mask. Luckily there’s a paper that blends the image with its surrounding context. It does require you to make mattes of the photoshopped part and define a feathering area. Realistic results nonetheless, although I like the colour of the simple style transfer version better.

The astute may have noticed that the portrait above was made in 1887 while Vincent cut off his ear in 1888. For those that value historical accuracy, I’ve made another style transfer image of a self-portrait of Vincent in 1889.

In the previous post about making text in Chaotica, I introduced the Sierpiński Gasket. I got a complaint about it not being centrally symmetrical. So I decided to make a version of the Gasket that will annoy those preoccupied with symmetry. As always here’s the code. Try and see what it does and how it works if you feel like it.

First off, let's answer the more important question: what is a gasket? My dictionary tells me it's supposed to be 'a flat piece of soft material or rubber that is put between two joined metal surfaces to prevent gas, oil or steam from escaping: The gasket has blown'. This seems to be a bit of a misnomer for an immaterial object that certainly isn't put in between something and with its infinite holes would surprise me if it could prevent anything liquid from ever escaping. Despite the misnomer, I do think fractal gaskets are beautiful and do not blow. Googling gasket leads to images that faintly resemble fractal gaskets. Another term often used is the Sierpiński sieve. The fractal could actually be a nice sieve that sorts grains of sand and has infinitely many hole sizes. On top of that, it also has a classy ring to it and from here on out, I will refer to gaskets as sieves.

Now we got that out of the way we can start answering the question on how to construct the fractal. Intuitively the sieve can be constructed using scissors by removing the same structure as the structure we had at the start, but flipped, rotated and scaled (note that these operations are exactly what affine transformations can do). What's left is three scaled-down versions of the original triangle. Now repeat this ad infinitum.

IFS operate on a pixel level. For IFS it is not a matter of cutting entire pieces out, but a matter of never reaching certain areas, a.k.a the void. With the exception of the first few iterations (due to the possibility of choosing a starting point that does not lie within the set), you will never reach some parts of the triangle. These parts do not belong to the set. Convince yourself by trying. For illuminating reasons, I give in and post the equilateral Sierpinski sieve. But only because this version makes it easy to spot the congruent little triangles it is made up out of. Each angle is 60 degrees. Each void is the same shape as the whole triangle, but scaled down twice and rotated. Because each angle is the same we don't have to worry about flipping operations.

Can this function set be generalised? According to the paper Sierpiński pedal triangles by Ding et al. it can. The general form is (don't forget to set your calculator to degrees):

   

   

   

This is where things start to get wonky. What if you use other values than three 60 degree angles? Below I used 50, 60 and 70 respectively. It's less obvious, but the void leaves three congruent triangles yet again. There's mathematical proof though it's easier to just take out your geo triangle to convince yourself once more. Can we recreate the sieve from the previous post? Unfortunately, we can't with this formula, it collapses to an ordinary filled triangle. It's not wonky enough. I encourage you to try other wonky values. Like what evens happens when the angles don't add up to 180? That would be crazy and should never be attempted.

Hope you enjoyed it! Spotted a mistake, please let me know at matigekunstintelligentie@gmail.com